Chemical Crystallography

The CRYSTALS 15.0.1 (v7809) installer for Windows 7/10 is now available. This is a quick patch release following the release of v7795.

Please report problems. The version number refers to a specific snapshot of the source code enabling us to better identify and fix bugs.

Key changes between 15.7795 and 15.7809

This is a small patch release which fixes a couple of broken URLs, adds some new icons, new shortcut keys, quick access to import and export via toolbar.

Key changes between 14.6999 and 15.7795

This release of CRYSTALS has changed the way the software is installed, so that you don’t need administrator permission to install or run it.
If you have an old version of CRYSTALS installed, and you follow the prompt to uninstall it, it will require administrator permissions. If you do not uninstall the old version there may be duplicated information in different parts of the registry, but it should not prevent use of the software.

The new install structure brings CRYSTALS closer to best practice for installing applications on Windows, and as a result you can no longer find the application and examples in c:\wincrys\

While this will be distressing for users from the days of the command line, it shouldn’t affect point-and-click users very much. Application and supporting files can be found in

%LOCALAPPDATA%\Programs\crystals

and demo files are in

%APPDATA%\crystals\demo

If you need to access demo files or edit CRYSTALS scripts, you can paste the locations above into a Windows Explorer, or find shortcuts to both of these locations in the Windows start menu in the Crystals group.

Other changes since v14.6999 (July 2018):

•  Added ‘cycle residue’ button to toolbar. Eases working with large structures. See: https://www.youtube.com/watch?v=sN7w-THNmTo
• Added ‘cycle parts’ button to help visualise disorder parts: https://youtu.be/OoRm9J7hfjE?t=268
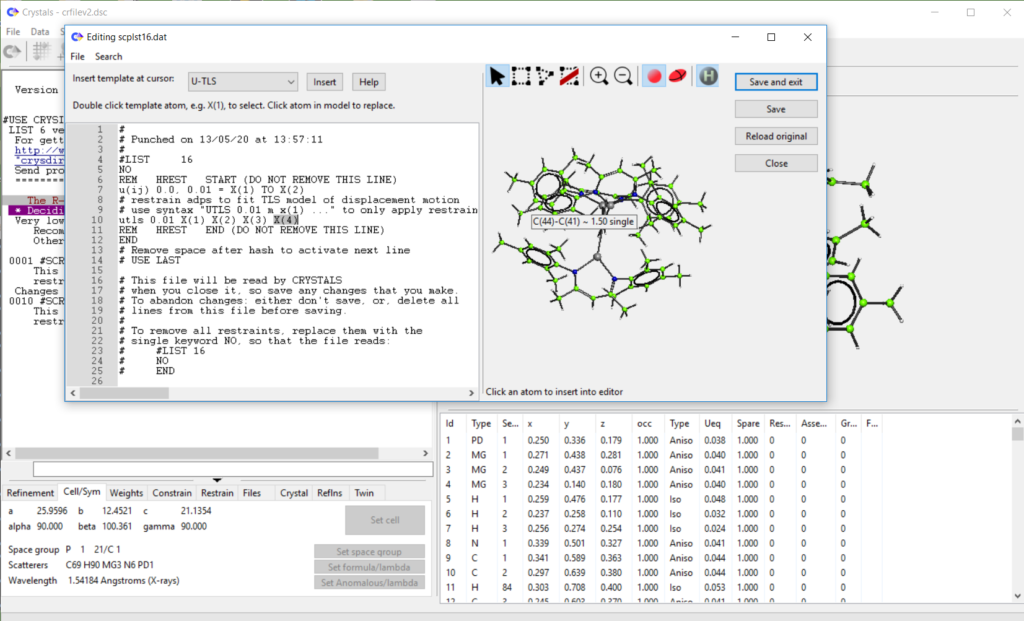
• Added ‘restrain templates’ to list 16 editor. Work in progress, see demo here: https://www.youtube.com/watch?v=R3SHqKv9pCg
• Improved refinement mode override for individual atoms. Video here: https://www.youtube.com/watch?v=sCTV4HN8RDk
• Catch instabilities during matrix inversion, allow user to choose precision or speed in GUI
• Improved undo structure dialog. Catch cases with lists marked as ‘in error’. Structure is shown automatically when selecting.
• Reflections with a weight of zero are excluded from the total count.
• Output files (listing, punch, mon) and many intermediate data files are now stored in subfolders of your working directory to keep it tidier.
• Additional colours added to colour tables for atom types.
• Removed dependency on CRYSDIR environment variable when launched from command line. Will override if set, but otherwise .exe location is used.
• Sort deuterium with H in CIF formula.
• Peak height slider added to find H dialog, use it to hide low density peaks. Improved usage with neutron H maps.
• Slant Fourier dialog now computes default size limits which encapsulate the selected atoms.
• Fix cell su issue when importing data from .ins files (and other bugfixes for edge cases in shelx2cry)
• Fix sorting of data in Mogul dialog window (regression)
• Fix reading of squeeze data from PLATON (regression)
• Fix Cameron (regression)
• Changed behaviour: if you click a link to a file in the working folder in CRYSTALS text window (e.g. publish.cif) it opens in Windows Explorer instead of the default application.
• Upgraded MCE.
• Text output simplified, especially SFLS.
• Added Find and Replace dialogs to internal text file editor (e.g. for editing L12 and L16).
• Updated icons.
• Get WinGX location from the registry rather than environment variable.
• Historically Fourier map units are scaled by 10.0 to give 10 x e-/A^3 (e.g. in MCE or MapView). Command line default remains same for compatibility, but the GUI difference Fourier dialog now uses a scale factor of 1.0
• Added logging of file closures in .log file – easier to track which script or input file commands were from.
• Shelx2cry will now automatically import hkl if given a path to a different folder.
• Some renaming of CIF data items for filtered sets of data for compatibility with CheckCIF. All output is still present, comments in CIF explain the reasoning.
• Added electron radiation type. Scattering factors (eight-term approximation) for electrons included L.-M. Peng (1999) Micron 30, 625-648.
• Remember preference (per-structure) for refining occupancy of PARTS when using the Guide (saves unchecking box for every refinement setup).
• Default CRYSTALS merge updated to ignore large outliers. Will effect some noisy datasets if they are re-imported. 
• Fixed Invert structure option in Structure menu.
• Fixed ‘change to uequiv’ popup menu 
• Fixed ‘set Uiso’ popup menu item 
• Many small bug fixes and improvements. Full commit history and changes at https://github.com/ChemCryst/crystals/

The CRYSTALS v6720 installer is now available.

This update uses a new 64-bit Fortran compiler, fixes a number of bugs and eliminates a few mysterious crashes. Please report problems. The version number now refers to a specific snapshot of the source code enabling us to better identify and fix bugs.

Key changes between v14.6237 and 14.6720
64-bit compiler, bundle mkl math libraries – improved stability. Updated icon.
Improved SHELX import for atoms on special positions, SADI, DFIX and MPLA restraints, long form factors.
Spot is_nan in plot data.
New set of displacement parameter restraints, including TLS.
Better #CHECK output for restraints – including individual leverages.
Fix misreport of symmetry operators in CIF for C2/m
Dynamic threshold of Q peak height in Fourier peak viewer script.
Allow paths containing single quotes.
Add greek symbols to text and graphs for more concise display.
Leverages calculation via #sfls, refine punch=leverages, end
Changes related to getting consistent results for Thmax in CIF
Fixed listbox operation clicking in list now generates appropriate feedback for scripts.
Least squares matrix condition number output now included for problem refinement diagnosis.
Avoid almost infinite loop looking for bonds if atom coords have gone bad. Side effect – bonds outside +/- 50 unit cells of the origin won’t be found.
New choice of matrix invertors for SFLS. Default can be set in L23.
Fix default hkl format when re-reading ‘from-cif.hkl’ files (3F4.0,2F10.0).
Add a few more instrument/diffractometer types (synchrotron, neutron sources, etc.)
Modify platanom calculation: (i) use more d.p for improved precision; (ii) use c and d terms to correct data with all anomalous scattering effect removed as detailed in final version of ‘HUG and SQUEEZE’ manuscript.
Compute dispersion correction terms and photon interaction cross section for non-standard (=Mo,Cu) wavelength data. Alter xinlist3 to streamline experience.
Undo dialog: fix situation where current L5 is marked as error list.
Check for isotropic / unknown atoms before attempting to SPLIT in xsplits.ssc
Make L11 depend on L28, now if L28 filters change the VCV becomes invalid, require re-refinement. Avoids publishing CIF after omitting reflections without extra cycles.
Fix storage of converge checkbox state so it isn’t overridden when called from xwrite5.
Edlist3: revamp user interface to simplify. Added get/set mu values from L29 for each element.
Add Helium to properties file.
LIST 6 version incremented to 124. NEW DSC files will not be backwards compatible with older versions of CRYSTALS.
Better treatment of twins in Fourier maps.
Fix output of RIDE constraints (better refinement stability).
Reduce decimal places for angles with no esd (e.g. by symmetry constraint, or not refined) from 3 to 2 in CIF output. Avoids reporting e.g. 179.995 degress for exactly 180 degree angles.
Add internal vs external variance plot
Fix switch on of extinction from the Guide ‘Add extinction parameter’ dialog.